Question

Suppose that x is the probability that a randomly selected person is left handed. The value (1-x) is the probability that the person is not left handed. In a sample of 1000 people, the function V(x)=1000x(1-x) represents the variance of the number of left-handed people in a group of 1000. What is the maximum variance?

Answer 1

The maximum variance is 250.

Explanation:

Consider the provided function.

`V(x)=1000x(1-x)`

`V(x)=1000x-1000x^2`

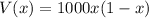
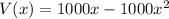
Differentiate the above function as shown:

`V'(x)=1000-2000x`

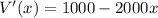
The double derivative of the provided function is:

`V''(x)=-2000`

To find maximum variance set first derivative equal to 0.

`1000-2000x=0`

`x=(1)/(2)`

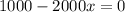
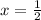
The double derivative of the function at
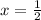`x=(1)/(2)` is less than 0.

Therefore,
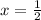`x=(1)/(2)` is a point of maximum.

Thus the maximum variance is:

`V(x)=1000((1)/(2))-1000{(1)/(2)}^2`

`V(x)=250`

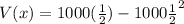
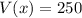
Hence, the maximum variance is 250.