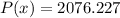Answer:
The Maximum value is
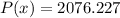
Explanation:
Given,
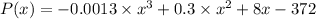 (equation-1)
(equation-1)
Differentiate above equation with respect to 'x',
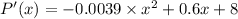 --- (equation 2)
--- (equation 2)
Again differentiate above equation with respect to 'x',
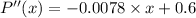 ------- (equation 3)
------- (equation 3)
From equation-2 we see,
The value of
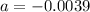 ,
,
 ,
,
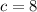 .
.
Now, for maximum or minimum, the first derivative must be 0.
For maximum,
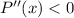
So,

Using the quadratic formula, we find the roots of



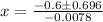
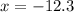 or
or
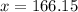
For
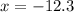 ,
,
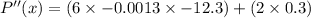

Which is minimum value at
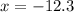
And for
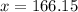 ,
,

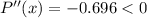
Which is maximum value at
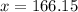
Plug
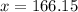 in equation-1,
in equation-1,
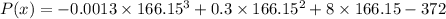
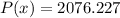
So the Maximum value is