Question

The sum of the first 10 terms of an arithmetic progression is 120 and the sum of first twenty is 840. find sum of first 30 terms​

Answer 1

The sum of first 30 terms of the arithmetic progression is 2160.

Step-by-step explanation:

For an arithmetic progression, the sum of first
`n` terms with first term as
`a` and common difference
`d` is given as:

`S_n=(n)/(2)(2a+(n-1)d)`

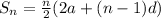
Now, it is given that:

`For\ n=10,S_n=120\\For\ n=20,S_n=840`

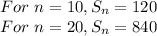
Now, plug in these values and frame two equations in
`a\ and\ d`

`S_(10)=(10)/(2)(2a+(10-1)d)\\120=5(2a+9d)\\2a+9d=(120)/(5)\\2a+9d=24------------1`

`S_(20)=(20)/(2)(2a+(20-1)d)\\840=10(2a+19d)\\2a+19d=(840)/(10)\\2a+19d=84-----------2`

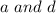
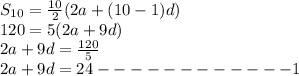
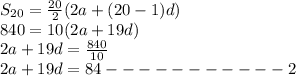
Now, we solve equations (1) and (2) for
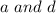`a\ and\ d`. Subtract equation (1) from equation (2). This gives,

`2a+19d-2a-9d=84-24\\19d-9d=60\\10d=60\\d=(60)/(10)=6`

Now, plug in the value of
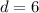`d=6` in equation (1) and solve for
`a`.

`2a+9(6)=24\\2a+54=24\\2a=24-54\\2a=-30\\a=(-30)/(2)=-15`

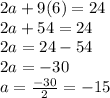
Plug in the values of
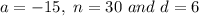`a=-15,\ n=30\ and\ d=6` in the sum formula to find the sum of first 30 terms.

Now, the sum of first 30 terms is given as:

`S_(30)=(30)/(2)(2(-15)+(30-1)(6))\\S_(30)=15(-30+29(6))\\S_(30)=15(-30+174)\\S_(30)=15(144)=2160`

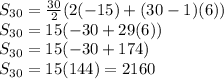
Therefore, the sum of first 30 terms of the arithmetic progression is 2160.