Question

Suppose that there are six prospective jurors, four men (M) and two women (W), who might be impaneled to sit on the jury in a criminal case. Two jurors are randomly selected from these six to fill the two remaining jury seats. (a) List the simple events in the experiment. (HINT: There are 15 simple events if you ignore the order of selection of the two jurors. Select all that apply.)

Answer 1

W1W2; W1M1; W1M2; W1M3; W1M4; W2M1; W2M2; W2M3; W2M4; M1M2; M1M3; M1M4; M2M3; M2M4; M3M4.

Explanation:

Applying combinatorial analysis, the total number of simple events is given by:

`E= (6!)/(2!(6-2)!)=(6*5*4!)/(2*4!)\\E= (6*5)/(2) = 15`

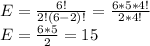
Let the four men be M1, M2 ,M3, M4 nad the two women W1 and W2

All of the possible events with W1 on the jury are:

W1W2; W1M1; W1M2; W1M3; W1M4;

The remaining possible events with W2 on the jury are:

W2M1; W2M2; W2M3; W2M4.

The remaining possible events with M1 on the jury are:

M1M2; M1M3; M1M4

The remaining possible events with M2 on the jury are:

M2M3; M2M4

The last possible event is:

M3M4