Question

Ship A is 32 miles north of ship B and is sailing due south at 16 mph. Ship B is sailing due east at 12 mph. At what rate is the distance between the ships changing an hour later? Are they getting closer together or farther apart?

Answer 1

-5.6 mi/h

Step-by-step explanation:

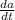`(da)/(dt)` = Velocity of ship A = -16 mi/h (negative as the distance is decreasing)

Distance ship A travels in 1 hour = 16×1 = 16 mi

a = Distance remaining = 32-16 = 16 mi

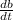`(db)/(dt)` = Velocity of ship B = 12 mi/h

b = Distance ship B travels in 1 hour = 18×1 = 12 mi

c = Distance between A and B after 1 hour = √(a²+b²) = √(16²+12²) = 20 mi

From Pythagoras theorem

a²+b² = c²

Now, differentiating with respect to time

`2a(da)/(dt)+2b(db)/(dt)=2c(dc)/(dt)\\\Rightarrow a(da)/(dt)+b(db)/(dt)=c(dc)/(dt)\\\Rightarrow (dc)/(dt)=(a(da)/(dt)+b(db)/(dt))/(c)\\\Rightarrow (dc)/(dt)=(18* 54+24* 72)/(90)\\\Rightarrow (dc)/(dt)=-5.6\ mi/h`

∴ Rate at which distance between the ships is decreasing one hour later is 5.6 mi/h