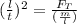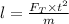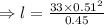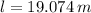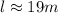Answer:
Step-by-step explanation:
Given:
Tension in the string,
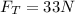
mass of the string,
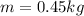
time taken to transmit the sound,
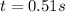
We have the relation of the given with velocity 'v' as:
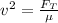 ................................(1)
................................(1)
where:
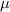 = linear mass density of the string=
= linear mass density of the string=
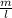
we know:
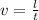
where:
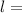 length of the string
length of the string
Putting the corresponding values in the eq. (1)