Question

The Genetics & IVF Institute conducted a clinical trial of the YSORT method designed to increase the probability of conceiving a boy. As of this writing, 291 babies were born to parents using the YSORT method, and 239 of them were boys. Use a 0.01 significance level to test the claim that the YSORT method is effective in increasing the likelihood that a baby will be a boy. What is the value of the test statistic needed to test this claim?

Answer 1

Answer: The test statistic needed to test this claim= 10.92

Explanation:

We know that the probability of giving birth to a boy : p= 0.5

i..e The population proportion of giving birth to a boy = 0.5

As per given , we have

Null hypothesis :
`H_0: p\leq0.5`

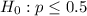
Alternative hypothesis :
`H_a: p>0.5`

Since
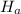`H_a` is right-tailed , so the hypothesis test is a right-tailed z-test.

Also, it is given that , the sample size : n= 291

Sample proportion:
`\hat{p}=(239)/(291)\approx0.82`

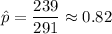
Test statistic :
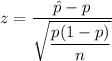`z=\frac{\hat{p}-p}{\sqrt{(p(1-p))/(n)}}` , where n is sample size ,
`\hat{p}` is sample proportion and p is the population proportion.

`\Rightarrow\ z=\frac{0.82-0.5}{\sqrt{(0.5(1-0.5))/(291)}}\approx10.92`

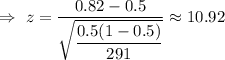
i.e. the test statistic needed to test this claim= 10.92

Critical value ( one-tailed) for 0.01 significance level =
`z_(0.01)=2.326`

Decision : Since Test statistic value (10.92)> Critical value (2.326), so we reject the null hypothesis .

[When test statistic value is greater than the critical value , then we reject the null hypothesis.]

Thus , we concluded that we have enough evidence at 0.01 significance level to support the claim that the YSORT method is effective in increasing the likelihood that a baby will be a boy.