Question

Based on historical data, your manager believes that 41% of the company's orders come from first-time customers. A random sample of 72 orders will be used to estimate the proportion of first-time-customers. What is the probability that the sample proportion is between 0.35 and 0.5?

Answer 1

1-.41=.59

Z(0.35)= (0.35-.41)/squa root of (.41*.59)/72=-1.035141128

Z(.5)=(.5-.41)/squa root of (.41*.59)/72=1.552711693

NorCDF on your calculator ( Znd, Vars, NorCdf):

NorCDF(-1.035, 1.55)= .78909

Explanation:

Answer 2

The probability that the sample proportion is between 0.35 and 0.5 is 0.7895

Explanation:

To calculate the probability that the sample proportion is between 0.35 and 0.5 we need to know the z-scores of the sample proportions 0.35 and 0.5.

z-score of the sample proportion is calculated as

z=
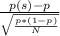`\frac{p(s)-p}{\sqrt{(p*(1-p))/(N) } }` where

• p(s) is the sample proportion of first time customers
• p is the proportion of first time customers based on historical data

• N is the sample size

For the sample proportion 0.35:

z(0.35)=
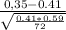`\frac{0,35-0.41}{\sqrt{(0.41*0.59)/(72) } }` ≈ -1.035

For the sample proportion 0.5:

z(0.5)=
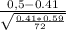`\frac{0,5-0.41}{\sqrt{(0.41*0.59)/(72) } }` ≈ 1.553

The probabilities for z of being smaller than these z-scores are:

P(z<z(0.35))= 0.1503

P(z<z(0.5))= 0.9398

Then the probability that the sample proportion is between 0.35 and 0.5 is

P(z(0.35)<z<z(0.5))= 0.9398 - 0.1503 =0.7895