Question

HELLLLLLP PLEASE CAN SOMEONE PLEASE EXPLAIN?

Consider parallelogram ABCD with vertices A(-6, 6), B(-2, 8), C(0, 4), and D(-4, 2). Classify the parallelogram and select ALL that apply.
Group of answer choices

ABCD is a rectangle.

ABCD is none of these.

ABCD is a rhombus.

ABCD is a square.

Answer 1

ABCD is a RHOMBUS or a SQUARE.

Explanation:

The coordinates are A(-6, 6), B(-2, 8), C(0, 4), and D(-4, 2).

By DISTANCE FORMULA:

The length of the segment with coordinates X(a,b) and Y(c,d) is given as:

`XY = √((c-a)^2  + (d-b)^2)`

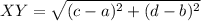
Now, similarly, the lengths of the segments are:

`AB = √((-2 -(-6))^2  + (8-6)^2)`

`=√((4)^2  + (2)^2)  = √(16 + 4)   = √(20)`

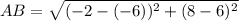
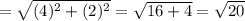
⇒ The length of the segment AB = √ 20 units

`BC = √((0 -(-2))^2  + (4-8)^2)`

`=√((2)^2  + (-4)^2)  = √(4 + 16)   = √(20)`

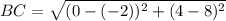
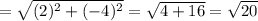
⇒ The length of the segment BC = √ 20 units

`CD = √((0 -(-4))^2  + (2-4)^2)`

`=√((4)^2  + (-2)^2)  = √(16 + 4)   = √(20)`

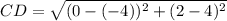
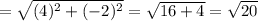
⇒ The length of the segment CD= √ 20 units

`AD = √((-6 -(-4))^2  + (6-2)^2)`

`=√((-2)^2  + (4)^2)  = √(4 + 16)   = √(20)`

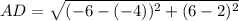
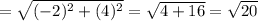
⇒ The length of the segment AD = √ 20 units

`AC = √((0 -(-6))^2  + (4-6)^2)`

`=√((6)^2  + (-2)^2)  = √(36 + 4)   = √(40)`

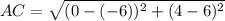
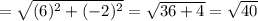
⇒ The length of the diagonal AC = √ 40 units

`BD = √((-2 +4)^2  + (8-2)^2)`

`=√((2)^2  + (6)^2)  = √(36 + 4)   = √(40)`

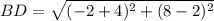
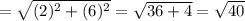
⇒ The length of the diagonal BD = √ 40 units

Since, here the length of all segments is √ 20 units.

⇒AB = BC = CD = AD = √ 20 units

and Diagonal AC = BD

⇒ ABCD is a RHOMBUS or SQUARE.