Question

Write the equation of a line that is perpendicular to y= 7/5 x +6 and that passes through the point 2,-6

Answer 1

The equation for line with point (2,-6) is given as : 5 x + 7 y = -32

Explanation:

The given equation of line 1 is y= 7/5 x +6

Comparing it with the form y = mx + C, we get m = 7/5.

So, the slope of the equation 1 is ( 7/5).

Now, let us assume the slope of line 2, which is perpendicular to line 1 is p.

⇒ Slope of line 1 x Slope of line 2 = -1 (as lines are perpendicular)

⇒ p x ( 7/5) = -1

⇒ p = - (5/7)

Also, a point online 2 is given as ( 2,-6).

By POINT SLOPE FORMULA:

The line of the equation with point (x0,y0) and slope m is given as:

y - y0 = m (x -x0)

So, here the line equation (2) is given as

`y - (-6)  = (-5)/(7) (x -2)\\\implies 7(y +6) = -5(x-2)\\\implies 7y + 42  = - 5x + 10\\\implies 5x + 7y = -32`

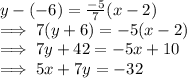
Hence, the equation for line 2 with point (2,-6) is given as : 5x + 7y = -32