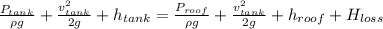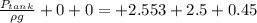Question

The closed tank of a fire engine is partly filled with water, the air space above being under pressure. A 6 cm bore connected to the tank discharges on the roof of a building 2.5 m above the level of water in the tank. The friction losses are of 45 cm of water. Determine the air pressure which must be maintained in the tank to deliver 20 litres/sec on the roof.

Answer 1

The air pressure in the tank is 53.9
`kN/m^(2)`

Solution:

As per the question:

Discharge rate, Q = 20 litres/ sec =
`0.02\ m^(3)/s`

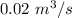
(Since, 1 litre =
`10^(-3) m^(3)`)

Diameter of the bore, d = 6 cm = 0.06 m

Head loss due to friction,
`H_(loss) = 45 cm = 0.45\ m`

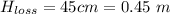
Height,
`h_(roof) = 2.5\ m`

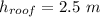
Now,

The velocity in the bore is given by:

`v = (Q)/(\pi ((d)/(2))^(2))`

`v = (0.02)/(\pi ((0.06)/(2))^(2)) = 7.07\ m/s`

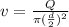
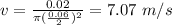
Now, using Bernoulli's eqn:

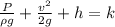`(P)/(\rho g) + (v^(2))/(2g) + h = k` (1)

The velocity head is given by:

`(v_(roof)^(2))/(2g) = (7.07^(2))/(2* 9.8) = 2.553`

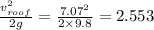
Now, by using energy conservation on the surface of water on the roof and that in the tank :

`(P_(tank))/(\rho g) + (v_(tank)^(2))/(2g) + h_(tank) = (P_(roof))/(\rho g) + (v_(tank)^(2))/(2g) + h_(roof) + H_(loss)`

`(P_(tank))/(\rho g) + 0 + 0 = \0 + 2.553 + 2.5 + 0.45`

`P_(tank) = 5.5* \rho * g`

`P_(tank) = 5.5* 1* 9.8 = 53.9\ kN/m^(2)`