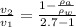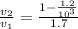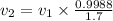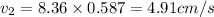Question

An aluminum sphere (specific gravity = 2.70) falling through water reaches a terminal speed of 8.36 cm/s. What is the terminal speed of an air bubble of the same radius rising through water? Assume viscous drag in both cases and ignore the possibility of changes in size or shape of the air bubble; Density of air at 20°c is 1.20 kg/m3 and that of water is 998.21 kg/m3.

Answer 1

Answer:4.91 cm/s

Step-by-step explanation:

Given

Specific Gravity
`=(\rho _s)/(\rho _w)=2.7`

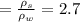
During falling velocity is
`v_1=8.36 cm/s`

Let during rising velocity be
`v_2`

Density of air
`\rho _a=1.20 kg/m^3`

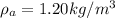
density of water
`\rho _w=998.21\approx 10^3 kg/m^3`

For Aluminium sphere

`m_1g=F_d+F_b`

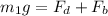
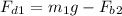`F_d_1=m_1g-F_b_2`-------1

For second case

`F_b_2=F_d_2+m_2g`

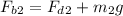
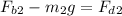`F_b_2-m_2g=F_d_2`----2

Divide 1 and 2 we get

`(F_d_2)/(F_d_1)=(F_b_2-m_2g)/(m_1g-F_b_2)`

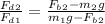
Drag force is given by
`6\pi \eta rv`

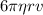
therefore

`(6\pi \eta rv_2)/(6\pi \eta rv_1)=(m_wg-m_2g)/(m_1g-m_wg)`

`(v_2)/(v_1)=(m_w-m_2)/(m_1-m_w)`

`(v_2)/(v_1)=(\rho _w-\rho _a)/(\rho _s-\rho _w )`

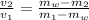
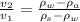
because
`mass=volume* density`

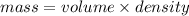
Taking
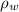`\rho _w` common

`(v_2)/(v_1)=(1-(\rho _a)/(\rho _w))/(2.7-1)`

`(v_2)/(v_1)=(1-(1.2)/(10^3))/(1.7)`

`v_2=v_1* (0.9988)/(1.7)`

`v_2=8.36* 0.587=4.91 cm/s`