Question

The capacity of an elevator is 15 people or 2400 pounds. The capacity will be exceeded if 15 people have weights with a mean greater than 2400/15=160 pounds. Suppose the people have weights that are normally distributed with a mean of 167 lb and a standard deviation of 29 lb. find the probability that if a person is randomly selected, his weight will be greater than 160 pounds.

Answer 1

0.5987

Explanation:

`\mu = 167`

`\sigma = 29`

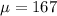
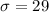
We are supposed to find the probability that if a person is randomly selected, his weight will be greater than 160 pounds.

Formula :
`Z=(x-\mu)/(\sigma)`

P(x>160)

Substitute the values in the formula :

`Z=(160-167)/(29)`

`Z=−0.241`

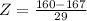
Refer the z table for p value

p value = 0.4013

P(x>160)= 1-P(x<160)=1-0.4013=0.5987

Hence the probability that if a person is randomly selected, his weight will be greater than 160 pounds is 0.5987