Step-by-step explanation:
It is known that relation between heat energy, specific heat and temperature change is as follows.
Q =
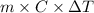
where, q = heat energy
m = mass
C = specific heat
 = change in temperature =
= change in temperature =
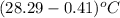 =
=
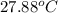
Therefore, calculate the heat energy as follows.
Q =
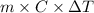
=

= 55292.06 J
or, = 55.3 kJ (as 1 kJ = 1000 J)
One ice cube is equal to 1 mole.
Hence, 6.020 kJ/mol of energy absorbed by 1 ice cube. And, number of ice cubes absorbing 55.3 kJ of energy will be calculated as follows.
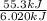
= 9
Thus, we can conclude that 9 ice cubes are necessary to cool the tea to
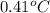 .
.