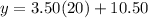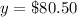Question

A carnival costs $10.50 to enter plus an additional $3.50 per ticket for rides and food.

Write an algebraic expression to represent the total cost for a visit to the carnival. Let n represent the number of tickets purchased.
​​What is the total cost to visit the fair if you purchase 20 tickets? Explain your reasoning.

Answer 1

`\$80.50`

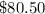
Explanation:

Let

n ----> represent the number of tickets purchased

y ---> the total cost for a visit to the carnival in dollars

we know that

The linear equation in slope intercept form is equal to

`y=m(n)+b`

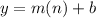
where

m is the slope or unit rate of the linear equation

b is the y-intercept or initial value

In this problem we have

The unit rate or slope is equal to

`m=\$3.50\ per\ ticket`

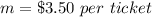
The y-intercept is equal to the cost for enter (value of y when the value of x is equal to zero)

`b=\$10.50`

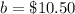
substitute

`y=3.50(n)+10.50`

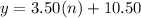
For n=20 tickets

substitute the value of n and solve for y

`y=3.50(20)+10.50`

`y=\$80.50`