Question

9. Water is added to two containers for 20 minutes. The equations below model the ounces of

water, y, in each container after x minutes. At the time when the containers hold the same
amount of water, how much water do they hold?
Container A: y=62x+48
Container B: y=-2x2 +80x+120
234 ounces
482 ounces
792 ounces
920 ounces

Answer 1

792 ounces

Explanation:

At the time when the containers hold the same amount of water the value of y in the equations is the same, so

`\large 62x+48=-2x^2+80x+120`

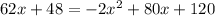
Solve the quadratic equation:

`\large 62x+48=-2x^2+80x+120\Rightarrow 2x^2-80x-120+62x+48=0\\\\2x^2-18x-72=0\Rightarrow x=(-(-18)\pm√((-18)^2-4(2)(-72)))/(2*2)=\\\\=(18\pm√(324+576))/(4)=(18\pm√(900))/(4)=(18\pm 30)/(4)`

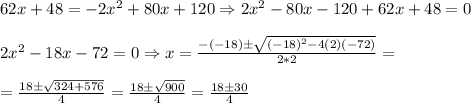
Take only the positive solution since x is positive (minutes)

`\large x=(18+30)/(4)=(48)/(4)=12`

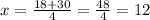
Now, compute the amount of water y by replacing x = 12 in any of the two equations, for example in container A which is easier to calculate

y = 62(12) + 48 = 792

The correct answer is then 792 ounces