Question

In a plane, points P and Q are 20 inches apart. If point R is randomly chosen from all the points in the plane that are 20 inches from P, what is the probability that R is closer to P than it is to Q?

A. 00
B. 1414
C. 1313
D. 1212
E. 23

Answer 1

E.
`(2)/(3)`

Explanation:

Consider a circle having centre P and radius 20 inches,

So, the area of the circle,

`A=\pi (20)^2\text{ square inches}`

Also, suppose points Q and R are on the circumference,

i.e. PQ = PR = 20 inches,

If QR = 20 inches,

So, triangle PQR is an equilateral triangle,

⇒ m∠RPQ = 60°,

Now, suppose R' is another point on the circle,

Such that, ΔPQR ≅ Δ PQR',

⇒ m∠QPR' = 60°,

Thus, minor angle, m∠RPR' = m∠RPQ + m∠QPR' = 60° + 60° = 120°,

⇒ major angle, m∠RPR' = 360° - 120° = 240°,

So, the area of the circle where a point on the circumference is closer to P than it is to Q

`=(240^(\circ))/(360^(\circ))\pi (20)^2`

`=(2)/(3)\pi (20)^2`

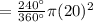
Hence, the probability that a point is closer to P than it is to Q =
`((2)/(3)\pi (20)^2)/(\pi (20)^2)`

`=(2)/(3)`

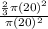
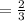
i.e. OPTION E is correct.