Question

The mayor of a town has proposed a plan for the construction of a new community. A political study took a sample of 900 voters in the town and found that 75% of the residents favored construction. Using the data, a political strategist wants to test the claim that the percentage of residents who favor construction is more than 72%. Testing at the 0.05 level, is there enough evidence to support the strategist's claim?

Answer 1

Answer with explanation:

Let p be the population proportion of residents who favor construction.

As per given , we have

Null hypothesis :
`H_0: p\leq0.72`

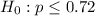
Alternative hypothesis :
`H_a: p>0.72`

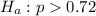
Since
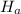`H_a` is right-tailed , so the hypothesis test is a right-tailed z-test.

Also, it is given that , the sample size : n= 900

Sample proportion:
`\hat{p}=0.75`

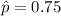
Test statistic :
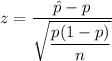`z=\frac{\hat{p}-p}{\sqrt{(p(1-p))/(n)}}` , where n is sample size ,
`\hat{p}` is sample proportion and p is the population proportion.

`\Rightarrow\ z=\frac{0.75-0.72}{\sqrt{(0.72(1-0.72))/(900)}}\approx2`

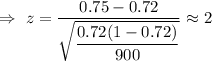
P-value (right tailed test)=P(z>2)=1-P(z≤2) [∵P(Z>z)=1-P(Z≤z)]

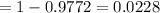`=1-0.9772=0.0228` [using p-value table of z.]

Decision : Since P-value (0.0228) < Significance level (0.05), so we reject the null hypothesis .

Thus , we concluded that we have enough evidence at 0.05 significance level to support the strategist's claim that the percentage of residents who favor construction is more than 72%.