Answer with explanation:
Formula for confidence interval for population mean ( if population standard deviation is unknown ) :
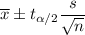
, where n= sample size
 = sample mean
= sample mean
s= sample standard deviation
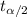 = two-tailed t-value for significance level of (
= two-tailed t-value for significance level of (
 ).
).
Let x denotes the amount of additional tax owed .
We assume that amount of additional tax owed is normally distributed .
As per given , we have
n= 64
Degree of freedom : df = 63 [ df= n-1]
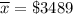
s= $2595
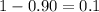
Using t-distribution table ,
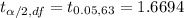
Then , 90% confidence interval for the mean additional amount of tax owed for estate tax returns would be :
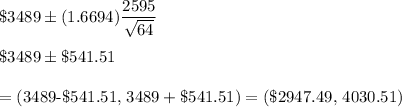
1) The lower bound is $2947.49 .
2) The upper bound is $4030.51 .
Interpretation : We are 90% confident that the true population mean amount of additional tax owed lies between $2947.49 and $4030.51.