Answer:
So
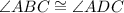
And

Explanation:
Given;
ABCD is a parallelogram and opposite sides of this parallelogram are parallel that is 'AB' parallel with 'DC' and 'BC' parallel 'AD'
Now joint the point 'A' and 'C' and we get two different triangle 'ABC' and 'ADC',
Reason: Given
 then mention that Alternate Interior angles are equal for parallel lines.
then mention that Alternate Interior angles are equal for parallel lines.
Reason: Given
 then mention that Alternate Interior angles are equal for parallel lines.
then mention that Alternate Interior angles are equal for parallel lines.
Reason: Common side.
Then

∴
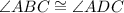
By using diagonal 'BD' we could flow similar argument to prove that
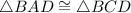 and also
and also

∴
