Question

The yield of orange trees is reduced if they are planted too close together. If there are 30 trees per acre, each tree produces 400 oranges. For each additional tree in the acre, the yield is reduced by 7 oranges per tree. How many trees per acre yield the largest crop for farmer Boyles?

Answer 1

5 more than 30 trees should be planted, for a total of 40 trees per acre.

Explanation:

Let x be the number of trees beyond 30 that are planted on the acre

The number of oranges produced = Oranges(x) = (number of trees) (yield per tree)

We are given that For each additional tree in the acre, the yield is reduced by 7 oranges per tree

So, number of oranges produced =
`(30 + x)(400 -10x)`

=
`12000 -300x+400x-10x^2`

=
`12000 + 100x-10x^2`

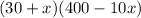
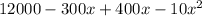
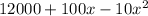
The derivative Oranges'(x) = 100-20x

Substitute first derivative equals to 0

`100-20x =0`

`x=5`

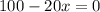
Using the second derivative test,

Oranges"(x) = -20

20 is negative,

So, this is the case of maximum.

Thus, 5 more than 30 trees should be planted, for a total of 40 trees per acre.