Question

Given that RH= 2.18 x 10⁻¹⁸J, 1 nm = 1 x 10⁻⁹m, h = 6.63 x 10⁻³⁴J·s, and c = 3.00 x 10⁸m/s:

Calculate the wavelength, innanometers, of the light emitted by a hydrogen atom during a transition of its electron from the n = 7 to the n = 3 principal energy level.

Answer 1

The wavelength the light emitted by a hydrogen atom during a transition is 1006 nm.

Step-by-step explanation:

By using Rydberg's Equation we cab determine the wavelength of the light:

`\Delta E=R_H* Z^2\left((1)/(n_i^2)-(1)/(n_f^2) \right )`

Where,

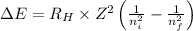
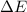`\Delta E` = Energy difference

`R_H` = Rydberg's Constant

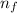`n_f` = Final energy level

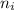`n_i`= Initial energy level

We have :
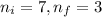`n_i=7,n_f=3` , Z = 1

`R_H=2.18* 10^(-18) J`

`\Delta E=2.18* 10^(-18) J* 1^2\left((1)/(7^2)-(1)/(3^2) \right )`

`\Delta E=1.9773* 10^(-19) J`

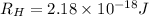
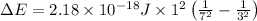
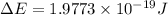
Now by using Plank's equation we can determine the wavelength of the light emitted.

`E=(hc)/(\lambda )`

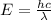
E = Energy of the emitted light

h = Planck's constant =
`6.63* 10^(-34) Js`

c = speed of light =
`3.00* 0^8 m/s`

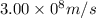
For the given transition the energy of the light = E

`E =1.9773* 10^(-19) J`

`\lambda=(hc)/(E)=(6.63* 10^(-34) Js* 3.00* 0^8 m/s)/(1.9773* 10^(-19) J)`

`\lambda =1.006* 10^(-6) m =1.006* 10^(-6)* 10^9=1006 nm`

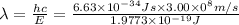
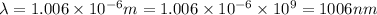
The wavelength the light emitted by a hydrogen atom during a transition is 1006 nm.