Question

Transforming between two encodings for Boolean vectors. A Boolean n-vector is one for which all entries are either 0 or 1. Such vectors are used to encode whether each of n conditions holds, with ai = 1 meaning that condition i holds. Another common encoding of the same information uses the two values −1 and +1 for the entries. For example the Boolean vector (0,1,1,0) would be written using this alternative encoding as (−1, +1, +1, −1). Suppose that x is a Boolean vector with entries that are 0 or 1, and y is a vector encoding the same information using the values −1 and +1. Express y in terms of x using vector notation. Also, express x in terms of y using vector notation.

Answer 1

See below

Explanation:

We are looking for a function f such that

f(0) = -1

f(1) = 1

One of the simplest ones is the line that joins (0, -1) and (1,1)

y = 2x -1

So, if we have a Boolean n-vector in the first codification (0,1)

`\large X=(x_1,x_2,...x_n)`

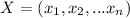
then

`\large (2x_1-1,2x_2-1,...2x_n-1)=(y_1,y_2,...,y_n) =Y`

is the expression of Y in terms of X.

Similarly, the inverse function of the line, x = (y+1)/2, does the inverse transformation.

That is to say, if we have a vector

`\large Y=(y_1,y_2,...,y_n)`

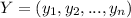
in the second codification -1 and +1

`\large ((y_1+1)/(2),(y_2+1)/(2),...(y_n+1)/(2))=(x_1,x_2,...x_n)=X`

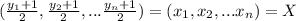
is the expression of X in terms of Y