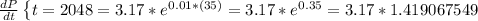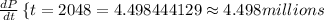Question

The United States population (in millions) is predicted to be P(t) = 317e0.01t, where t is the number of years after 2013.† Find the instantaneous rate of change of the population in the year 2048.

Answer 1

`(dP)/(dt) \left \{ {{t=2048} =4.498millions`

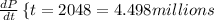
Explanation:

In order to find the instantaneous rate of change of the population in the year 2048 it is necessary to derivate the function P(t), so:

`(dP(t))/(dt) =317*0.01*e^(0.01t) =3.17*e^(0.01t)`

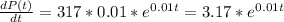
Now, let's find the total of years between 2013 and 2048:

`2048-2013=35`

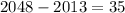
Finally, let's evaluate the derivative function at t=35

`(dP)/(dt) \left \{ {{t=2048} = 3.17*e^(0.01*(35)) =3.17*e^(0.35)=3.17*1.419067549\\`

`(dP)/(dt) \left \{ {{t=2048} = 4.498444129 \approx4.498millions`