Question

At a point 50 feet from the base of a church, the angles of elevation to the bottom of the steeple and the top of the steeple are 35° and 48°, respectively. Find the height of the steeple.

Answer 1

11.81 Km

Step-by-step explanation:

Considering when an airplane is 10 Km high so that the angle of depression to the towns lying directly to the East of plane are 28 and 55 as shown in the attached sketch

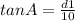`tan A=\frac {d1}{10}` hence
`d1=10tan 35^(\circ)=7.002075382\approx 7 Km`

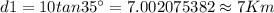
Also, angle B=35+(55-28)=62

`tan 62^(\circ)=\frac {d2}{10}`

`d2=10tan 62^(\circ)=18.80726465\approx 18.81 Km`

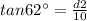
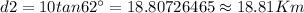
The distance between the two towns will be

18.81-7=11.81 Km