Question

PLEASE HELP!!!!! 3, 8, 13, 18, 23, ....

The recursive formula for this sequence is:

Answer 1

a₈ = 37

Explanation:

The given arithmetic sequence is: 3, 8, 13, 18, 23, . . .

The recursive formula for the sequence is:
`$ a_n = a_(n - 1) + 5 $`

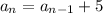
Here,
`$<strong> a_n</strong> $` represents the
`$ <strong>n^(th</strong>) $` of the sequence.

And,
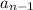`$ a_(n - 1) $` represents the
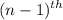`$ (n - 1)^(th) $` of the sequence.

'+5' denotes that '5' is added to the
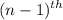`$ (n - 1)^(th) $` term to get the
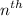`$ n^(th) $` term. In other words, the difference between two consecutive numbers in the sequence is 5.

Now, we are asked to find a₈ i.e., n =8.

Substituting in the recursive formula we get: a₈ = a₍₈₋ ₁₎ + 5 = a₇ + 5.

So, to determine a₈ we need to know a₇. From the sequence we see that a₅ = 23.

⇒ a₆ = 23 + 5 = 28.

⇒ a₇ = 28 + 5 = 32.

⇒ a₈ = 32 + 5 = 37.

Therefore, the
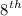`$ 8^(th) $` term of the sequence is 37.