Question

The amount of time that a drive-through bank teller spend on acustomer is a random variable with μ= 3.2 minutes andσ=1.6 minutes. If a random sample of 64 customers is observed,find the probability that their mean ime at the teller's counteris(a) at most 2.7 minutes.(b) more than 3.5 minutes.(c) at least 3.2 minutes but less than 3.4 minutes.

Answer 1

μ= 3.2 minutes

σ=1.6 minutes

a ) Find the probability that their mean time at the teller's counter is at most 2.7 minutes.

`P(x \leq 2.7)`

`Z=(x-\mu)/(\sigma)`

`Z=(2.7-3.2)/(1.6)`

`Z=-0.3125`

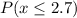
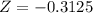
Refer the z table for p value

p value = 0.3783

Hence the probability that their mean time at the teller's counter is at most 2.7 minutes is 0.3783

b)Find the probability that their mean time at the teller's counter more than 3.5 minutes.

`P(x >3.5)`

`Z=(x-\mu)/(\sigma)`

`Z=(3.5-3.2)/(1.6)`

`Z=0.1875`

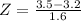
Refer the z table for p value

p value = 0.5714

P(x>3.5)=1-P(x<3.5)=1-0.5714=0.4286

Hence the probability that their mean time at the teller's counter more than 3.5 minutes is 0.4286

c)Find the probability that their mean time at the teller's counter at least 3.2 minutes but less than 3.4 minutes.

`P(3.2 \leq x\leq 3.5)`

`Z=(x-\mu)/(\sigma)`

`Z=(3.2-3.2)/(1.6)`

`Z=0`

Refer the z table for p value

p value = 0.5

`Z=(x-\mu)/(\sigma)`

`Z=(3.5-3.2)/(1.6)`

`Z=0.1875`

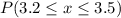
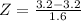
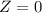
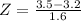
Refer the z table for p value

p value = 0.5714

`P(3.2 \leq x\leq 3.5)=P(x<3.5)-P(x<3.2)=0.5714-0.5=0.0714`

Hence the probability that their mean time at the teller's counter at least 3.2 minutes but less than 3.4 minutes is 0.0714