Question

What are the discontinuity and zero of the function f(x) = quantity x squared plus 5 x plus 4 end quantity over quantity x plus 4?

a Discontinuity at (−4, −3), zero at (−1, 0)

b Discontinuity at (−4, −3), zero at (1, 0)

c Discontinuity at (4, 3), zero at (−1, 0)

d Discontinuity at (4, 3), zero at (1, 0)

Answer 1

Option a - Discontinuity at (−4, −3), zero at (−1, 0)

Explanation:

Given : Function
`(x^2+5x+4)/(x+4)`

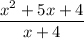
To find : What are the discontinuity and zero of the function ?

Solution :

To find the discontinuity for our given function
`(x^2+5x+4)/(x+4)`

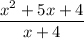
We will equate denominator to 0,

`x+4=0`

`x=-4`

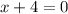
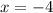
Now we simplify the expression,

`f(x)=(x^2+5x+4)/(x+4)`

`f(x)=((x+4)(x+1))/((x+4))`

`f(x)=x+1`

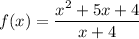
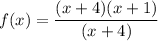
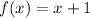
Since the denominator term is cancelled out, so our give function has a removable discontinuity.

Now, we will find value of y by substituting x=-4 in function
`f(x)=x+1`.

`f(-4)=-4+1`

`f(-4)=-3`

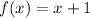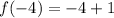
The discontinuity of given function is at point (-4,-3) .

For zeros of the function put function equate to zero.

`x+1=0`

`x=-1`

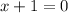
The zero is at (-1,0).

Therefore, Option a is correct.