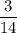
Explanation:
Given,number of red markers=
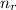 =4
=4
number of green markers=
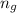 =8
=8
number of blue markers=
 =3
=3
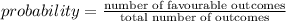
Let
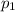 be the probability of getting a red marker=
be the probability of getting a red marker=
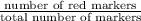
So,
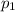 =
=
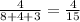
Let
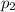 be the probability of getting a blue marker after getting a red marker.
be the probability of getting a blue marker after getting a red marker.
After removing a red marker,
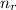 becomes 3 and
becomes 3 and
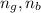 remain same.
remain same.
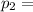
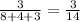
Probability for getting a red marker followed by getting a blue marker is
