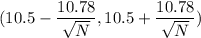Question

Samples (X1, X2, …. XN ) are taken from a normal distribution with unknown population mean and population variance. The sample mean is 10.5 and the sample variance is 5.5. What is the 95% confidence interval for the population mean?

Answer 1

Answer: 95% confidence interval would be

`(10.5-(10.78)/(√(N)),10.5+(10.78)/(√(N)))`

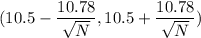
Explanation:

Since we have given that

Sample mean = 10.5

Sample variance = 5.5

Sample size = N

We need to find the 95% confidence interval for the mean.

z = 1.96

So, the confidence interval would be

`\bar{x}\pm z(\sigma)/(√(n))\\\\=10.5\pm 1.96(5.5)/(√(N))\\\\=(10.5-(10.78)/(√(N)),10.5+(10.78)/(√(N)))`

Hence, 95% confidence interval would be

`(10.5-(10.78)/(√(N)),10.5+(10.78)/(√(N)))`