Answer:
The directrix of parabola
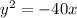 is the line x = +10.
is the line x = +10.
Explanation:
The general form of parabola is given as
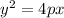
where the directrix is the vertical line x = - p .
If p > 0, then parabola opens to the right.
If p < 0 then parabola opens to the left.
Now here, the given equation is
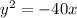
Representing the given equation in standard form:

⇒ p = -10
So, the directrix of the parabola is x = - p = - (-10) = 10
or, x = + 10
Hence, the directrix of parabola
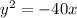 is the line x = +10.
is the line x = +10.