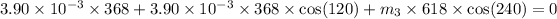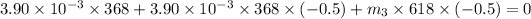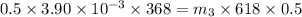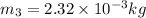Answer:

Step-by-step explanation:
Given
mass of first and second bullet
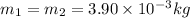
Velocity of two bullets
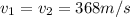
velocity of third bullet
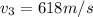
angles between guns is

Suppose First gun is at
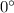 and second is at
and second is at
 and third is at
and third is at
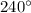
therefore
conserving momentum in x-direction
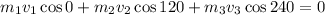
as three bullets club together to become lump