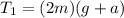Answer:
Part a)
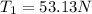

Part b)
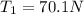
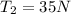
Part c)

Step-by-step explanation:
Part a)
As we know that the elevator is accelerating downwards
so we have force equation for sphere A given as

also for second sphere we have
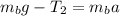
from above equations we have
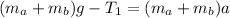

so we have
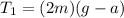

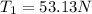
Now from other equation we have
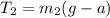
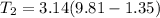

Part b)
Now the elevator is accelerating upwards
so we have force equation for sphere A given as
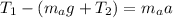
also for second sphere we have

from above equations we have
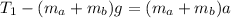
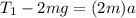
so we have
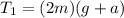

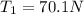
Now from other equation we have

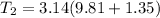
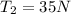
Part c)
Now we know that maximum possible tension in the string is
T = 92.6 N
so we have