1 Answer

Underyx · Answer 1 · 2020-01-27T08:16:05+0000

For this case we have that by definition, the equation of a line of the point-slope form is given by:

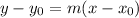
$y-y_ {0} = m (x-x_ {0})$

Where:

m: It's the slope

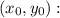$(x_ {0}, y_ {0}):$ It is a point through which the line passes

To find the slope, we need two points through which the line passes, observing the image we have:

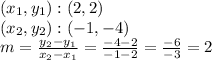
$(x_ {1}, y_ {1}): (2,2)\\(x_ {2}, y_ {2}): (-1, -4)\\m = \frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}} = \frac {-4-2} {- 1-2} = \frac {-6} {- 3} = 2$

Thus, the equation is of the form:

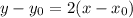
$y-y_ {0} = 2 (x-x_ {0})$

We choose a point:

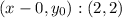
$(x- {0}, y_ {0}) :( 2,2)$

Finally, the equation is:

y-2 = 2 (x-2)

Now, we write the equation of the standard form
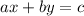ax + by = c :

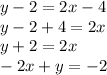
$y-2 = 2x-4\\y-2 + 4 = 2x\\y + 2 = 2x\\-2x + y = -2$

This is equivalent to:

2x-y = 2

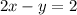
Answer:

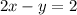
Option C

Please log in or register to add a comment.