Question

Multiple-Concept Example 4 and Conceptual Example 3 are pertinent to this problem. A bubble, located 0.200 m beneath the surface in a glass of beer, rises to the top. The air pressure at the top is 1.01 ???? 10 5 Pa. Assume that the density of beer is the same as that of fresh water. If the temperature and number of moles of CO2 in the bubble remain constant as the bubble rises, find the ratio of the bubble’s volume at the top to its volume at the bottom.

Answer 1

Step-by-step explanation:

The given data is as follows.

`P_(top) = 1.01 * 10^(5)`

`P_(bottom) = 1.01 * 10^(5) + \rho_(water) gh`

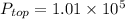
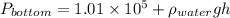
As, density =
`\rho * g * h`

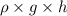
Now, putting the given values into the above formula as follows.

`P_(bottom) = 1.01 * 10^(5) + 1000 * 9.8 * 0.2 m`

=
`1.0296 * 10^(5)`

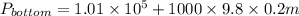
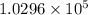
According to ideal gas equation, PV = nRT

And, in the given case PV = nRT = constant

Hence, calculate the volume ratio of top and bottom as follows.

`(V_(top))/(V_(bottom))` =
`(P_(bottom))/(P_(top))`

=
`(1.0296 * 10^(5))/(1.01 * 10^(5))`

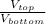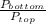
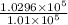
= 1.019

Thus, we can conclude that the ratio of the bubble’s volume at the top to its volume at the bottom is 1.019.