Answer:
There are no possible solutions
Explanation:
Given:
Minimum number of coins Alexa has =28 coins
Number of quarters Alexa has = 17 quarters
Total amount in coins = $5.05 = 505 cents
Let number of dimes be =
 coins
coins
So we can have two inequalities.
1) Total number of coins
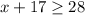 [Since minimum number of coins=28]
[Since minimum number of coins=28]
2) Total value of coins
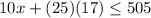 [As 1 dime=10 cents and 1 quarter=25 cents]
[As 1 dime=10 cents and 1 quarter=25 cents]
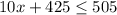
Solving inequality (1)
Subtracting both sides by 17.
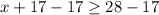
∴

Solving inequality (2)
Subtracting both sides by 425.
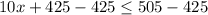

Dividing both sides by 10.

∴

On combining both solutions
 and
and
 ,
,
we see that there are no possible solutions as number of dimes cannot be ≥11 and ≤8 at the same time.