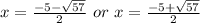Answer:
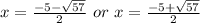
Explanation:
Given:
The equation to solve is given as:
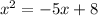
Rearrange the given equation in standard form
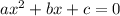 , where,
, where,
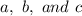 are constants.
are constants.
Therefore, we add
 on both sides to get,
on both sides to get,
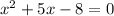
Here,
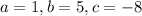
The solution of the above equation is determined using the quadratic formula which is given as:

Plug in
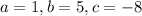 and solve for
and solve for
 .
.
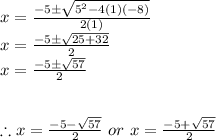
Therefore, the solutions are: