52
Explanation:
Let the number of fruit trees planted additionally be

Initially it is given that there are
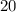 trees.
trees.
Number of trees after planting
 additional trees is
additional trees is
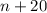
Let the yield due to each tree after planting
 additional trees be
additional trees be

Initially it is given that
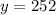
Yield due to each tree after planting
 trees is
trees is
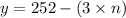
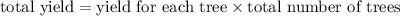
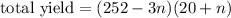
=
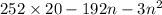
To maximise yield,we take that value of
 for which
for which
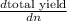
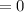
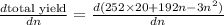 =
=

So,
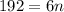 and
and

So,32 additional trees has to be planted to maximise yield.
So,there should be 52 trees in total