Question

Three cards are lined up on a table. Each card has a letter printed on one side

and a positive number printed on the other side. One card has an R printed on
it, one card has a G printed on it, and one card has a B printed on it. The
number side of each card is facedown on the table. The following is known about
the three concealed numbers:

(i) the product of the number on the card with an R and the number on the
card with a G equals the number on the card with a B;
(ii) the product of the number on the card with a G and the number on the card
with a B is 180; and
(iii) five times the number on the card with a B equals the number on the card
with a G.

Determine the product of the numbers on the three cards.

Answer 1

Product of the numbers on three cards is 36 .

Explanation:

Let the numbers on the cards with R , G , B respectively be, x , y and z.

Then, according to the question, we get the following 3 equations,

xy = z ----------- (1)

yz = 180 ------------(2)

5z = y ------------(3)

so, from (3) we get, z = y/5 -----------(4)

Putting the value of z from (4) in (2) we get,

`y^(2) = 900`

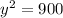
⇒ y = 30 [since, y > 0] ------------(5)

So, from (5) and (3) we get,

z = 30/5 = 6 ------------------(6)

so, from (1) we get, xyz =
`z^(2)`

=
`6^(2)`

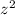
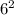
= 36