Question

Find the sum of the first five terms of the geometric series 1+3+9+...

A. 40
B. 121
C. 364
D. 1093

Answer 1

The sum of
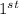`1^(st)` five terms of the series is 121.

Option - B

SOLUTION:

Given that, we have to find the sum of the first five terms of the geometric series 1 + 3 + 9 + ...

We already know, first three terms, let us find next two terms also.

`\text { Then, common ratio }=\frac{\text { second term of series }}{\text { first term series }}=(3)/(1)=3`

Now, we know that,
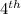`4^(th)` term is
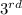`3^(rd)` term multiplied by the common ratio so,
`4^{\text {th }} \text { term }=9 * 3 \rightarrow 4^{\text {th }} \text { term }=27`

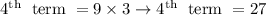
And,
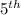`5^(th)` term is
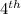`4^(th)` term multiplied by common ratio. So,
`5^{\text {th }} \text { term }=27 * 3 \rightarrow 5^{\text {th }} \text { term }=81`

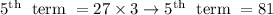
Now, sum of first five terms =
`1 + 3 + 9 + 27 + 81 = 4 + 36 + 81 = 40 + 81 = 121`

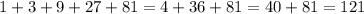
Hence, the sum of
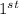`1^(st)` five terms of the series is 121.

Answer 2

Good evening ,

Answer:

B. 121

Explanation:

1×3=3

3×3=9

9×3=27

27×3=81

the sum = 1+3+9+27+81 = 121.

:)