Question

A 50.0 kg crate is being pulled along a horizontal, smooth surface. The pulling force is 10.0 N and is directed 20.0 degree above the horizontal. Find the normal force the crate and the magnitude of the acceleration of the crate. A. 250 N, 0.0684 m/s^2B. 487 N, 0.188 m/s^2 C. 525 N, 0.200 m/s^2 D. 825 N, 0.376 m/s^2 E. 494 N, 0.0728 m/s^2

Answer 1

Step-by-step explanation:

It is given that,

Mass of the crate, m = 50 kg

Force acting on the crate, F = 10 N

Angle with horizontal,
`\theta=20^(\circ)`

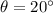
Let N is the normal force acting on the crate. Using the free body diagram of the crate. It is clear that,

`N=mg-F\ sin\theta`

`N=50* 9.8-10\ sin(20)`

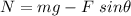
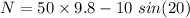
N = 486.57 N

or

N = 487 N

If a is the acceleration of the crate. The horizontal component of force is balanced by the applied forces as :

`ma=F\ cos\theta`

`a=(F\ cos\theta)/(m)`

`a=(10* \ cos(20))/(50)`

`a=0.1879\ m/s^2`

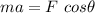
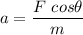
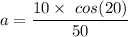
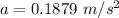
or

`a=0.188\ m/s^2`

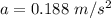
So, the normal force the crate and the magnitude of the acceleration of the crate is 487 N and
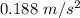`0.188\ m/s^2` respectively.