Question

A 19.3 kg dog is running northward at 2.98 m/s , while a 6.26 kg cat is running eastward at 3.64 m/s . Their 78.7 kg owner has the same momentum as the two pets taken together. You may want to review. Find the direction and magnitude of the owner's velocity.

Answer 1

v = 0.78 m/sec at 21.61° towards the east of north

Step-by-step explanation:

Given a 19.3 kg dog is running northward at 2.98 m/s , while a 6.26 kg cat is running eastward at 3.64 m/s and the mass of the owner is 78.7 kg.

Given m(dog) = 19.3 kg and m(cat) = 6.26 kg

v(dog) =
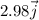`2.98\vec{j}` m/sec

v(cat) =
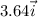`3.64\vec{i}` m/sec

Given the
`\vec{P}(owner)=\vec{P}(dog)+\vec{P}(cat)`

Let the velocity of the owner be
`\vec{v}`

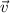
We know that
`\vec{P}=m\vec{v}`

`m(owner)* \vec{v}=m(dog)* \vec{v(dog)}+m(cat)* \vec{v(cat)}`

`78.7* \vec{v}=19.3* 2.98\vec{j}+6.26* 3.64\vec{i}`

`\vec{v}=(1)/(78.7)(57.5\vec{j}+22.78\vec{i})`

`v=\sqrt{((57.5)/(78.7))^2+((22.78)/(78.7))^2  }`

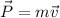
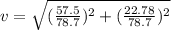
v=0.78 m/sec

for direction

Tan(α)=
`(component of x)/(component of y)`

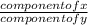
where α is the angle toward east of north.

Tan(α)=
`(22.78)/(57.5)`

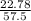
α=21.61°