Let's analyze the changes made to the parent function one by one:
STEP 1: Horizontal translation.
If we transform
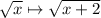
We're performing a change in the form of
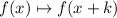
This kind of changes result in a horizontal translation, k units to the left if k is positive, k units to the right if k is negative. In this case, k=2, so the original graph is shifted 2 units to the left.
STEP 3: Vertical stretch.
If we transform

We're performing a change in the form of
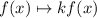
This kind of changes result in a vertical stretch with scale factor k. If k is negative, the function is also reflected across the x axis. In this case, k=3, so the original graph is stretched vertically, with scale factor 3.
STEP 3: Vertical translation.
If we transform
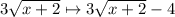
We're performing a change in the form of
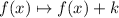
This kind of changes result in a vertical translation, k units down if k is positive, k units up if k is negative. In this case, k= -4, so the graph is shifted 4 units down.
All, in all, the original graph is shifted 2 units to the right, then it's stretched vertically with scale 3, and then it's shifted 4 units down. The order is important!