Answer:
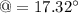
Step-by-step explanation:
It is given that,
Radius of the banked road, r = 400 m
Speed of the car for the safe travelling, v = 35 m/s
On the banking of a curve, the force of friction is balanced by the centripetal force acting on it such that the banking angle is given by :
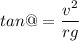
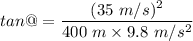
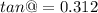
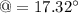
So, the banking angle of the road is 17.32 degrees. Hence, this is the required solution.