Question

Water flows from the bottom of a storage tank at a rate of r(t) = 200 − 4t liters per minute, where 0 ≤ t ≤ 50. Find the amount of water that flows from the tank during the first 30 minutes.

Answer 1

Answer: The amount of water is 4200 liters during the first 30 minutes.

Explanation:

Since we have given that

Water flows at the rate of

`r(t)=200-4t` liters per minute.

Here, t is the number of minutes

We need to find the amount of water that flows from the tank during the first 30 minutes.

So, t = 30.

So, our equation becomes,

`V=\int\limits^(30)_0 {200-4t} \, dt\\\\V=200t-4(t^2)/(2)|_0^(30)\\\\V=200(30)-2(30)^2\\\\V=6000-1800\\\\V=4200`

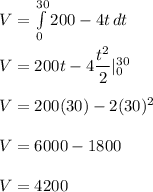
Hence, the amount of water is 4200 liters during the first 30 minutes.