Question

At the beach, Kate collects sea shells of mass 100 g and places them in a bucket. She swings the bucket in a large circle (radius 0.4 m), vertical with the ground, so that the bucket swings over her head. When the bucket is at the top of the circle, upside down, the tangential velocity of the shells is 4 m/s. The sea shells do not fall out of the bucket. What is the net force on the sea shells inside the bucket at this poin

a. The net force is the same as the force of gravity.
b. The net force is the same as the centripetal force.
c. The net force is zero because the force of gravity cancels the centripetal force and the shells do not fall out of the bucket.
d. The net force is the centripetal force plus the force of gravity since both are acting downward when the bucket is at the top of the circle.

Answer 1

b. The net force is the same as the centripetal force.

Step-by-step explanation:

When bucket is revolving in circle of constant radius then the net force at any moment of time is always towards the center of the circle which is given as

`F = (mv^2)/(R)`

`m = 0.100 kg`

`v = 4 m/s`

`R = 0.4 m`

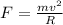
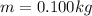
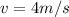
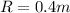
now we have

`F = (0.100(4^2))/(0.4)`

`F = 4 N`

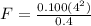
while the weight of the sea shell is given as

`W = mg`

`W = 0.100 * 9.81`

`W = 0.981 N`

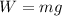
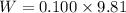
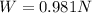
so here net force is more than the weight which means it must have normal force along with the weight of sea shells at that position

so correct answer will be

b. The net force is the same as the centripetal force.