Question

∠ACE is formed by two secants intersecting outside of a circle. If minor arc BD = 25°, minor arc AB = 115°, and minor arc DE = 115°, what is the measure of ∠ACE?

Answer 1

m∠ACE = 40°

Explanation:

Consider the below figure attached with this question.

Given information: arc BD = 25°, minor arc AB = 115°, and minor arc DE = 115°.

We need to find the measure of ∠ACE.

minor arc AB + minor arc BD + minor arc DE + minor arc AE = 360°

115° + 25° + 115° + minor arc AE = 360°

255° + minor arc AE = 360°

minor arc AE = 360° - 255°

minor arc AE = 105°

The measure of minor arc AE is 105°.

Using Intersecting secants outside the circle theorem

Angle between two secants =
`(1)/(2)`(Major arc - Minor arc)

`\angle ACE=(1)/(2)[Arc(AE)-Arc(BD)]`

`\angle ACE=(1)/(2)[105-25]`

`\angle ACE=(1)/(2)[80]`

`\angle ACE=40`

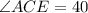
Therefore, the measure of ∠ACE is 40°.