Question

Tom rented a truck for one day. There was a base fee of $18.99, and there was an additional charge of 75 cents for each mile driven. Tom had to pay $160.74 when he returned the truck. For how many miles did he drive the truck?

Answer 1

Tom drove the truck for a distance of 89 miles.

Explanation:

Base fee of truck = $18.99

Additional charge per mile = $0.75 per mile

Amount paid by Tom for the rented truck = $160.74

Let us assume Tom drove the truck for a distance of
`m` miles.

So, for
`m` miles they would charge in dollars as:

⇒
`\textrm{ Base fee+ (Additional charge times miles driven) }`

⇒
`18.99+(0.75* m)`

⇒
`18.99+0.75\ m`

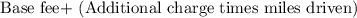
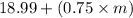
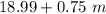
We know the actual amount charge, so we can equate.

`18.99+0.75\ m=160.74`

Subtracting both sides by 18.99 to cancel 18.99 on left side.

`18.99+0.75\ m-18.99=160.74-18.99`

`0.75\ m=160.74-18.99`

`0.75\ m=141.75`

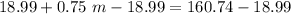
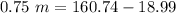
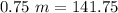
dividing both sides by 0.75 to isolate
`m`

`(0.75\ m)/(0.75)=(141.75)/(0.75)`

`m=89`

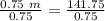
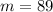
∴ Tom drove the truck for a distance of 89 miles.