Answer:
C = 19 is the minimum value
Explanation:
Sketch the inequalities using
4x + 3y = 29
with x- intercept = (7.25, 0) and y- intercept = (0,
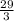 )
)
x + 2y = 11
with x- intercept = (11, 0) and y- intercept = (0. 5.5)
Solve 4x + 3y and x + 2y = 11 simultaneously to find
Point of intersection = (5, 3)
The vertices of the feasible region are
(0,
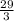 ), (5, 3), (11, 0)
), (5, 3), (11, 0)
Evaluate the objective function C = 2x + 3y at each of the vertices
(0,
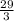 ) → C = 0 + 29 = 29
) → C = 0 + 29 = 29
(5, 3) → C = 2(5) + 3(3) = 10 + 9 = 19 ← minimum value
(11, 0) → C = 2(11) + 0 = 22
Minimum value is C = 19 when x = 5 and y = 3