Answer:
We check to verify that the step
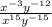 is included in simplifying the expression.
is included in simplifying the expression.
Thus, option D is correct.
Explanation:
Given the expression
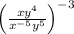
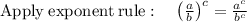
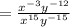 ← This is the step
← This is the step
Thus, the step
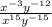 is included in simplifying the expression.
is included in simplifying the expression.
Thus, option D is correct.
BONUS!
LET US SOLVE THE REMAINING
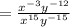
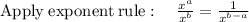
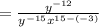
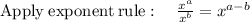
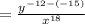
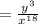
From the above calculations, we check to verify that the step
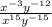 is included in simplifying the expression.
is included in simplifying the expression.
Thus, option D is correct.